预备知识 (Preliminaries)
1. 深度学习模型
- 深度神经网络(DNN):由多层全连接层组成,每层后接激活函数(如ReLU)。
- 卷积神经网络(CNN):局部感受野和参数共享机制,适合提取空间结构特征。
- 长短期记忆网络(LSTM):特殊的循环神经网络(RNN),能有效捕捉时间序列的长期依赖信息。
2. 高斯过程回归(Gaussian Process Regression)
高斯过程是一种非参数贝叶斯模型,定义在函数空间上。对于输入$x$,高斯过程给出:
$$
f(x) \sim \mathcal{GP}(m(x), k(x,x’))
$$
其中$m(x)$为均值函数,$k(x,x’)$为协方差函数。本文使用带线性均值项和RBF核的高斯过程:
$$
g(x) = f(x) + h(x)^T \beta
$$
其中$\beta$为线性权重,$f(x)$为零均值高斯过程。
核函数形式:
$$
k_{\text{SE}}(x, x’) = \sigma^2 \exp\left( -\frac{||x - x’||^2}{2r^2} \right)
$$
观测带噪声,因此核函数实际形式为:
$$
k(x,x’) = k_{\text{SE}}(x,x’) + \sigma_e^2 \delta_{x,x’}
$$
其中$\delta$为Kronecker delta函数。
1. 引言 (Introduction)
作物产量预测对于缓解全球粮食安全问题和优化农业生产至关重要。传统预测方法通常依赖地面调查和专家经验,但这类方法成本高昂,且在数据稀缺的地区(如发展中国家)难以推广。
随着遥感技术的发展,利用卫星数据进行作物产量预测成为可能。MODIS等卫星系统可以提供高频次、覆盖全球的植被指数和地表温度数据。但原始遥感数据高维且复杂,如何有效提取信息仍是一大挑战。
为此,本文提出了一种基于深度神经网络与高斯过程结合的深度高斯过程(Deep Gaussian Process, DGP)模型,用于从遥感影像中自动学习表征并建模空间相关性,提升作物产量预测准确性。
本文的主要贡献包括:
- 端到端特征学习:用深度神经网络(CNN或LSTM)直接从直方图表示的遥感数据中学习特征,避免人工特征设计。
- 直方图输入建模:将遥感数据编码为区域像素分布直方图,简化输入,同时保留空间信息。
- 高斯过程残差建模:在深度特征之上叠加高斯过程,建模地理邻近区域的空间残差结构。
2. 数据与预处理 (Data and Preprocessing)
2.1 数据来源
本研究使用了两类主要数据源:
- 作物产量数据:来自美国农业部国家农业统计服务(USDA NASS),提供2003-2015年间美国11个州县级大豆产量数据。
- 遥感数据:来自MODIS传感器,采集多时相植被指数(如NDVI)和地表温度(LST)。
2.2 处理流程
- 时间选取:生长季(5月至10月),每8天一个时间步,提取相关影像。
- 空间裁剪:依据县级行政边界裁剪MODIS影像,仅保留农业用地区域。
- 特征提取:
- 计算归一化植被指数(NDVI):
$$
\text{NDVI} = \frac{\text{NIR} - \text{RED}}{\text{NIR} + \text{RED}}
$$
- 计算归一化植被指数(NDVI):
- 缺失数据处理:对受云层遮挡的数据点进行插值和标准化处理。
- 直方图编码:将每个县在每个时间步的遥感数据,编码为单变量直方图,描述像素值的分布。每张直方图归一化,以消除县域面积差异影响。
- 最终输入:每个县的输入是随时间变化的一系列直方图,形成时间序列特征。
3. 方法
3.1 模型框架
本文设计的深度高斯过程模型由两个主要模块组成:深度神经网络特征提取模块和高斯过程回归模块。深度神经网络负责从多时相遥感影像中提取空间和时间特征,高斯过程利用这些特征建模空间相关性并进行产量预测。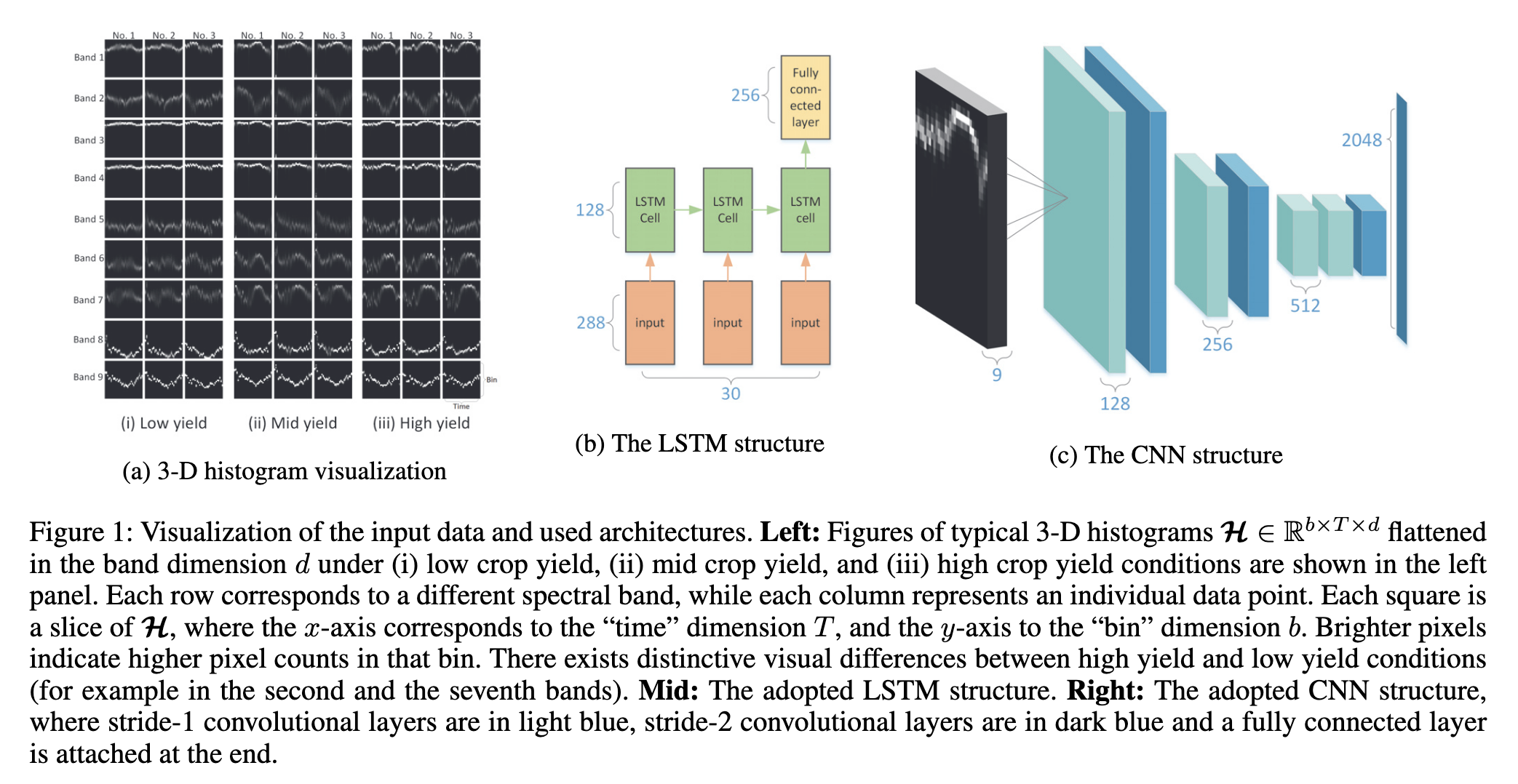
3.2 特征提取网络
- 空间特征提取(CNN):多层卷积和池化操作提取局部空间信息,生成低维空间表示。
- 时间动态建模(LSTM):对提取的空间特征序列进行时间依赖建模,捕获作物生长的时序变化。
3.3 高斯过程回归
将深度神经网络输出的特征作为输入,高斯过程利用RBF核函数建模特征之间的空间相关性。通过最大化边缘似然联合训练神经网络和GP超参数,实现端到端学习。
3.4 损失函数与训练
采用负对数边缘似然作为损失函数,结合Adam优化器进行参数更新。训练过程中,深度神经网络和高斯过程参数共同优化,提高模型泛化能力和不确定性估计准确性。
4. 实验设计与评估
4.1 实验设置 (Experimental Setup)
- 直方图表示:每个时间步,将NDVI数值划分为20个区间,构建单变量直方图,形成时间序列输入。
- CNN设置:
- 输入尺寸:$64 \times 64 \times C \times T$,其中$C$是通道数,$T$是时间步。
- 卷积核大小:$3 \times 3$。
- 激活函数:ReLU。
- 优化器:Adam,初始学习率0.001。
- LSTM设置:
- 每个时间步输入一个特征向量(直方图)。
- 两层堆叠LSTM单元,分别为128和64个隐藏单元。
- Dropout比例0.5。
- 高斯过程设置:
- 核函数:RBF核。
- 超参数初始化:$\sigma_f^2=1.0$,长度尺度$l=1.0$,噪声方差$\sigma_n^2=0.1$。
- 使用GPflow实现高斯过程训练。
- 训练策略:
- 留一年出交叉验证(Leave-One-Year-Out Cross Validation, LOYO-CV)。
- 每年单独作为测试集,其余年份作为训练集。
4.2 评估指标 (Evaluation Metrics)
均方根误差 (RMSE):
$$
\text{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 }
$$平均绝对误差 (MAE):
$$
\text{MAE} = \frac{1}{n} \sum_{i=1}^n | y_i - \hat{y}_i |
$$决定系数 ($R^2$ Score):
$$
R^2 = 1 - \frac{\text{RSS}}{\text{TSS}}
$$其中,
$$
\text{RSS} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
$$$$
\text{TSS} = \sum_{i=1}^{n} (y_i - \bar{y})^2
$$
4.3 Baseline
为了评估提出的深度高斯过程方法的有效性,本文设置了以下基线(baseline)模型进行对比:
- Ridge Regression:带有L2正则化的线性回归模型,作为传统机器学习方法的代表。
- Decision Tree Regression:基于非参数决策树的回归模型,能捕捉特征之间的非线性关系。
- Deep Neural Network (DNN):标准的多层感知器(MLP)网络,输入为遥感直方图特征,独立预测每个县的产量。
- Convolutional Neural Network (CNN):基于卷积操作建模空间局部相关性,直接从直方图特征中学习空间特征。
- Long Short-Term Memory (LSTM):基于时间序列建模的循环神经网络(RNN)变种,学习作物生长季节的动态变化模式。
此外,本文还评估了将高斯过程(GP)模块结合在深度特征之上的增强模型:
- CNN + GP:在CNN输出特征的基础上,叠加高斯过程以建模空间残差。
- LSTM + GP:在LSTM输出特征的基础上,叠加高斯过程以建模空间残差。
通过与这些Baseline模型的系统对比,本文验证了深度特征学习与空间建模联合提升产量预测精度的效果。
4.4 年份对比实验
表1:按年份的RMSE比较(县级预测性能,数值越低越好)。
| 年份 | Ridge | Tree | DNN | LSTM | LSTM+GP | CNN | CNN+GP |
|---|---|---|---|---|---|---|---|
| 2011 | 9.00 | 7.98 | 9.97 | 5.83 | 5.77 | 5.76 | 5.70 |
| 2012 | 6.95 | 7.40 | 7.58 | 6.22 | 6.23 | 5.91 | 5.68 |
| 2013 | 7.31 | 8.13 | 9.20 | 6.39 | 5.96 | 5.50 | 5.83 |
| 2014 | 8.46 | 7.50 | 7.66 | 6.42 | 5.70 | 5.27 | 4.89 |
| 2015 | 8.10 | 7.64 | 7.19 | 6.47 | 5.49 | 6.40 | 5.67 |
| Avg | 7.96 | 7.73 | 8.32 | 6.27 | 5.83 | 5.77 | 5.55 |
- 每一年,CNN+GP几乎始终取得最低的RMSE。
为了证明GP具有减少空间相关的误差的能力,作者绘制了2014年的CNN模型的预测误差。如下图,很明显,误差在空间上是相关的(红色表示低估和蓝色的含义过高的含义过高)。添加GP组件后,相关性降低。直观地,我们认为错误是由于遥感图像中无法观察到的属性(例如,由于土壤)。 GP部分从过去的培训数据中学习了这些模式,并有效地纠正了这些模式。
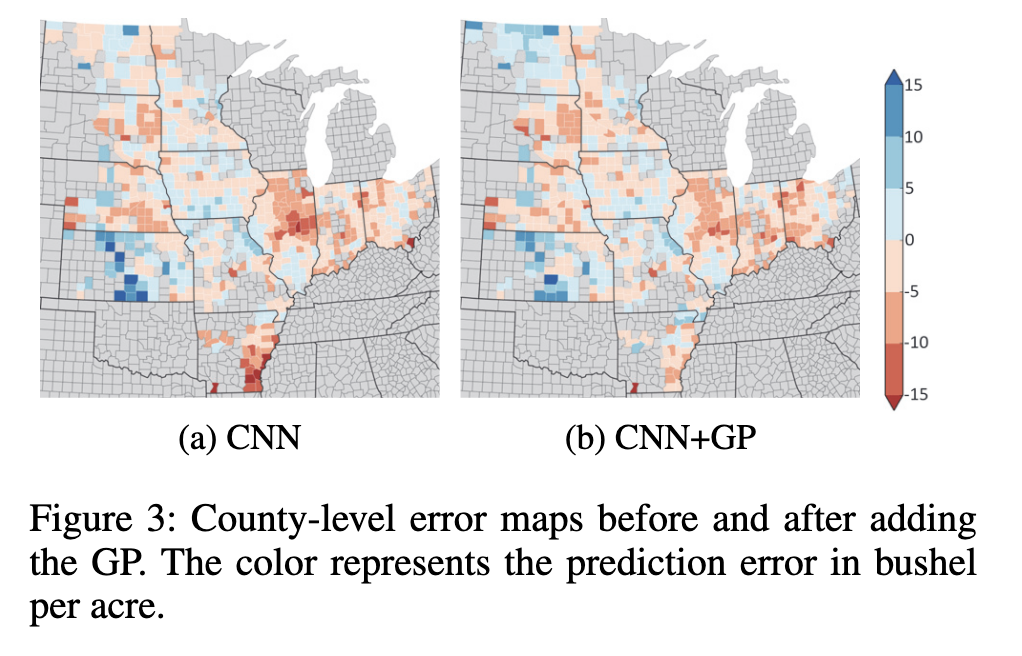
4.5 时间动态分析
逐月计算预测的MAPE变化,结果如下:
表2:美国层面作物产量预测的MAPE表现(2009–2015年均值)。
| 月份 | July (Ours) | August (USDA) | August (Ours) | September (USDA) | September (Ours) | October (USDA) | October (Ours) |
|---|---|---|---|---|---|---|---|
| MAPE (%) | 5.65 | 3.92 | 3.37 | 4.14 | 3.41 | 2.48 | 3.19 |
同时绘制了随时间变化的实时预测RMSE曲线:
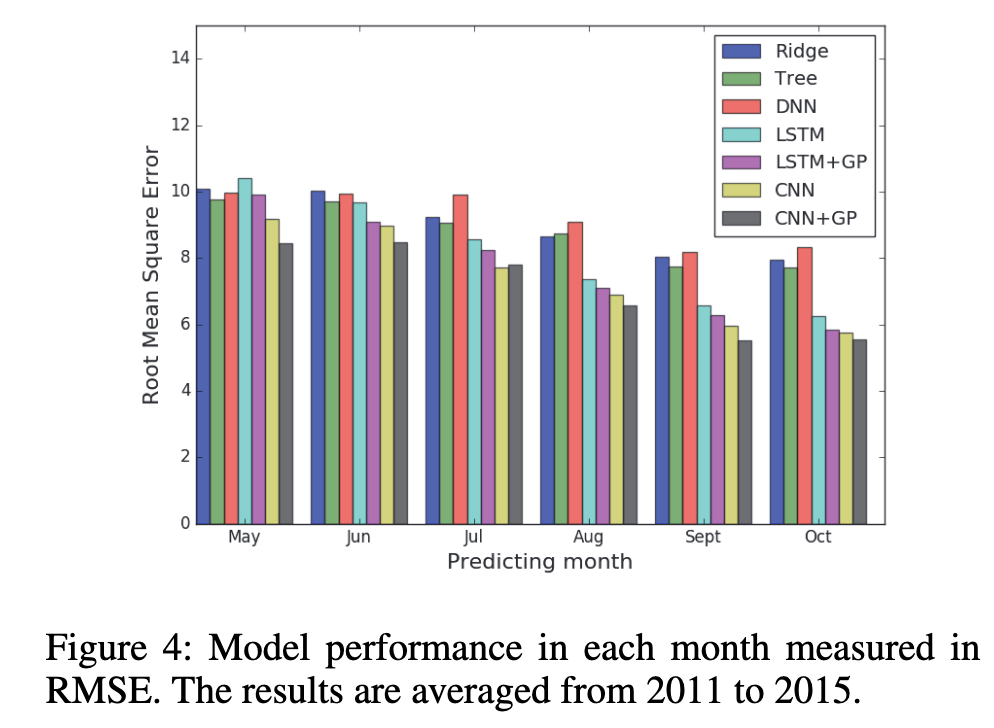
- 可以看到,从7月中旬(作物开花期)开始,预测误差迅速下降,到9月进入平台期。
- 提前预测的可行性较强,8月底已有接近全年最终准确率。
4.6 特征重要性分析
使用特征置换分析不同波段和时间点的重要性。
按波段重要性:
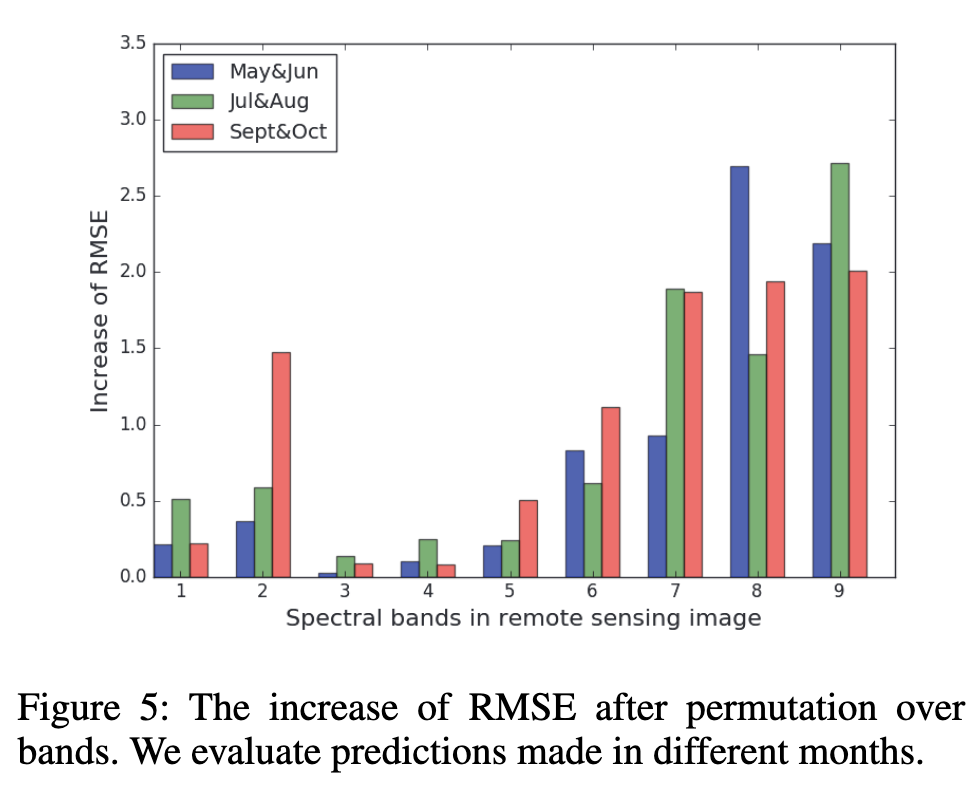
- NDVI和地表温度(LST)是最重要的两个特征。
按时间步重要性:
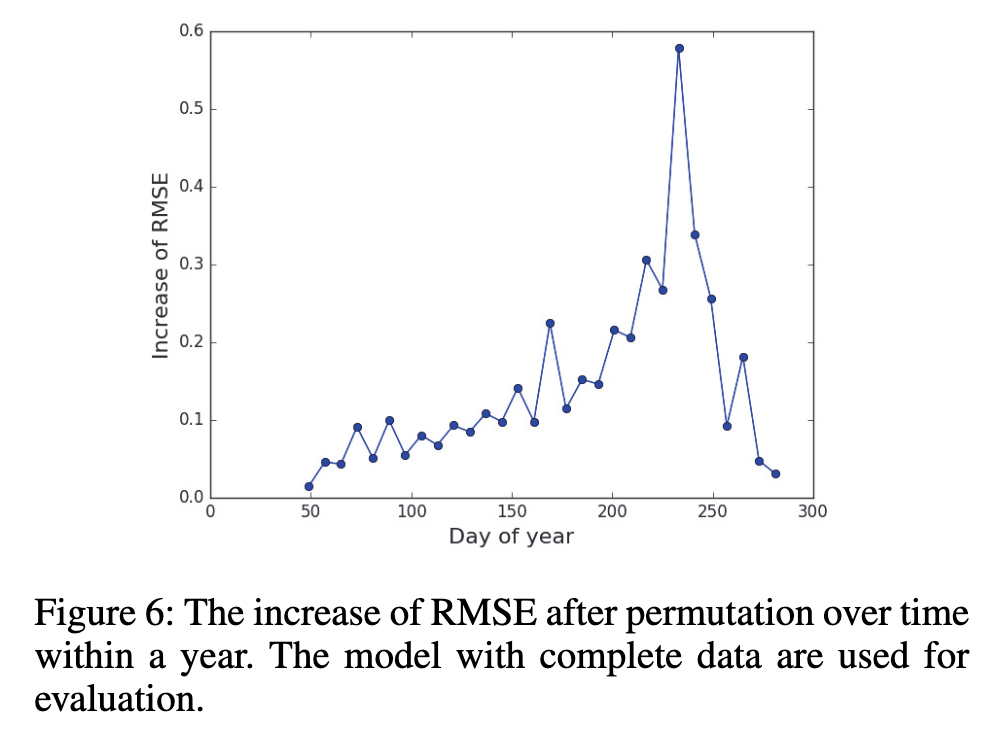
- 8月(开花和结荚期)的NDVI变化对最终产量预测贡献最大。
5. 结论 (Conclusion)
本文提出了结合深度神经网络与高斯过程的作物产量预测方法,创新性地使用直方图特征和空间相关性建模,在美国大豆数据集上显著提升了预测精度。
实验验证了:
- 特征学习比手工特征更有效;
- 高斯过程能有效捕捉地理邻近区域间的空间关系;
- 结合空间+时间动态建模可实现更早期、准确的产量预测。
参考文献
[1] Jiaxuan You, Xiaocheng Li, Melvin Low, David Lobell, Stefano Ermon. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 31, no. 1, 2017. [Online]. Available: https://ojs.aaai.org/index.php/AAAI/article/view/11172