1. 数据集背景与特点

MNIST数据集是机器学习领域中最常用的手写数字识别数据集之一。它包含60000张训练图像和10000张测试图像，每张图像的大小为28x28像素，共有10个类别（0到9）。MNIST数据集的广泛应用使得它成为了深度学习模型的测试基准之一。

让我们先看看数据集中的一些示例图像：

MNIST数据集示例

上图展示了数据集中的10个数字示例，每个数字都是28x28的灰度图像。这些图像经过预处理，像素值已经归一化到[-1, 1]区间。

本文假设读者已经对卷积神经网络(CNN)有基本了解。如果您对CNN的基本原理和组件不熟悉，建议先阅读我的CNN综述文章，其中详细介绍了CNN的发展历程、基本组件（如卷积层、池化层、激活函数等）以及经典CNN架构（如LeNet-5、AlexNet、VGG、GoogLeNet和ResNet）和现代CNN架构（如DenseNet、MobileNet和EfficientNet等）。本文将重点关注CNN在MNIST手写数字识别任务中的具体应用，包括模型设计、训练过程和性能分析，以及CNN如何通过层次化特征学习实现手写数字识别。

2. 理论基础

2.1 损失函数：交叉熵

在多分类问题中，我们通常使用交叉熵损失函数。交叉熵衡量了预测概率分布与真实分布之间的差异。对于单个样本，交叉熵损失的计算公式为：

$$L = -\sum_{i=1}^{C} y_i \log(\hat{y}_i)$$

其中：

  • $C$ 是类别数（在MNIST中为10）
  • $y_i$ 是真实标签的one-hot编码（目标类为1，其他类为0）
  • $\hat{y}_i$ 是模型预测的概率分布（经过softmax函数处理）

交叉熵损失的特点：

  • 当预测值接近真实值时，损失接近0
  • 当预测值偏离真实值时，损失值增大
  • 通过最小化交叉熵，模型学习到更准确的预测

2.2 优化器：Adam

Adam（Adaptive Moment Estimation）是一种自适应学习率的优化算法，它结合了动量（Momentum）和RMSprop的优点。Adam的更新规则如下：

$$m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t$$
$$v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2$$
$$\hat{m}_t = \frac{m_t}{1-\beta_1^t}$$
$$\hat{v}t = \frac{v_t}{1-\beta_2^t}$$
$$\theta_t = \theta{t-1} - \alpha\frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon}$$

其中：

  • $g_t$ 是当前梯度
  • $m_t$ 是一阶矩估计（梯度的移动平均）
  • $v_t$ 是二阶矩估计（梯度平方的移动平均）
  • $\beta_1, \beta_2$ 是衰减率（通常取0.9和0.999）
  • $\alpha$ 是学习率
  • $\epsilon$ 是小常数，防止除零

Adam优化器的优点：

  • 自适应学习率，不同参数有不同的更新步长
  • 结合了动量，可以处理稀疏梯度
  • 对超参数的选择相对不敏感

3. 模型设计与实现

3.1 环境配置和数据加载

首先，我们需要导入必要的库并设置数据加载：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import torch
import torch.nn as nn
import torchvision.transforms as transforms
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader

# 数据预处理
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

# 加载数据集
train_data = MNIST('./data', train=True, transform=transform, download=True)
test_data = MNIST('./data', train=False, transform=transform, download=True)

# 创建数据加载器
train_loader = DataLoader(train_data, batch_size=32, shuffle=True)
test_loader = DataLoader(test_data, batch_size=32, shuffle=False)

3.2 CNN模型架构

我们使用了一个包含三层卷积和三层全连接层的CNN模型。每个卷积层后都跟着ReLU激活函数和最大池化层。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class MnistModel(nn.Module):
    def __init__(self):
        super(MnistModel, self).__init__()
        self.conv1 = Conv2d(in_channels=1, out_channels=32, kernel_size=3, stride=1, padding=1)
        self.maxpool1 = MaxPool2d(2)
        self.conv2 = Conv2d(in_channels=32, out_channels=64, kernel_size=3, stride=1, padding=1)
        self.maxpool2 = MaxPool2d(2)
        self.conv3 = Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=1, padding=1)
        self.maxpool3 = MaxPool2d(2)
        self.fc1 = Linear(in_features=128*3*3, out_features=128)
        self.fc2 = Linear(in_features=128, out_features=64)
        self.fc3 = Linear(in_features=64, out_features=10)
        self.ReLU = ReLU()

    def forward(self, x):
        x = self.ReLU(self.maxpool1(self.conv1(x)))
        x = self.ReLU(self.maxpool2(self.conv2(x)))
        x = self.ReLU(self.maxpool3(self.conv3(x)))
        x = x.view(x.size(0), -1)
        x = self.fc1(x)
        x = self.fc2(x)
        x = self.fc3(x)
        return x

3.3 网络结构分析

让我们详细分析每一层的输出尺寸变化：

  1. 输入层：28×28×1

  2. 第一卷积层（Conv1）：

    • 输入：28×28×1
    • 卷积：3×3核，步长1，填充1
    • 输出：28×28×32
    • 最大池化：2×2，步长2
    • 最终输出：14×14×32

  3. 第二卷积层（Conv2）：

    • 输入：14×14×32
    • 卷积：3×3核，步长1，填充1
    • 输出：14×14×64
    • 最大池化：2×2，步长2
    • 最终输出：7×7×64

  4. 第三卷积层（Conv3）：

    • 输入：7×7×64
    • 卷积：3×3核，步长1，填充1
    • 输出：7×7×128
    • 最大池化：2×2，步长2
    • 最终输出：3×3×128

这就解释了为什么全连接层的输入维度是$12833=1152$。让我们用卷积和池化的输出尺寸计算公式来验证每一层的输出尺寸：

  1. 第一卷积层：

    • 卷积：$H_{out} = \left\lfloor \frac{28 - 3 + 2×1}{1} \right\rfloor + 1 = 28$
    • 池化：$H_{out} = \left\lfloor \frac{28 - 2}{2} \right\rfloor + 1 = 14$

  2. 第二卷积层：

    • 卷积：$H_{out} = \left\lfloor \frac{14 - 3 + 2×1}{1} \right\rfloor + 1 = 14$
    • 池化：$H_{out} = \left\lfloor \frac{14 - 2}{2} \right\rfloor + 1 = 7$

  3. 第三卷积层：

    • 卷积：$H_{out} = \left\lfloor \frac{7 - 3 + 2×1}{1} \right\rfloor + 1 = 7$
    • 池化：$H_{out} = \left\lfloor \frac{7 - 2}{2} \right\rfloor + 1 = 3$

4. 训练与评估

4.1 训练过程

训练过程中，我们使用了交叉熵损失函数和Adam优化器：

1
2
criterion = CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

训练过程的损失变化如下图所示：

训练损失曲线

从图中可以看出，模型的损失值随着训练步数的增加而稳定下降，表明训练过程正常。

4.2 预测结果分析

下面是模型在测试集上的一些预测结果：

预测结果示例

绿色表示预测正确，红色表示预测错误。从图中可以看出，模型对大多数数字都能正确识别。

4.3 模型性能评估

最后，让我们看看模型在各个数字上的识别准确率：

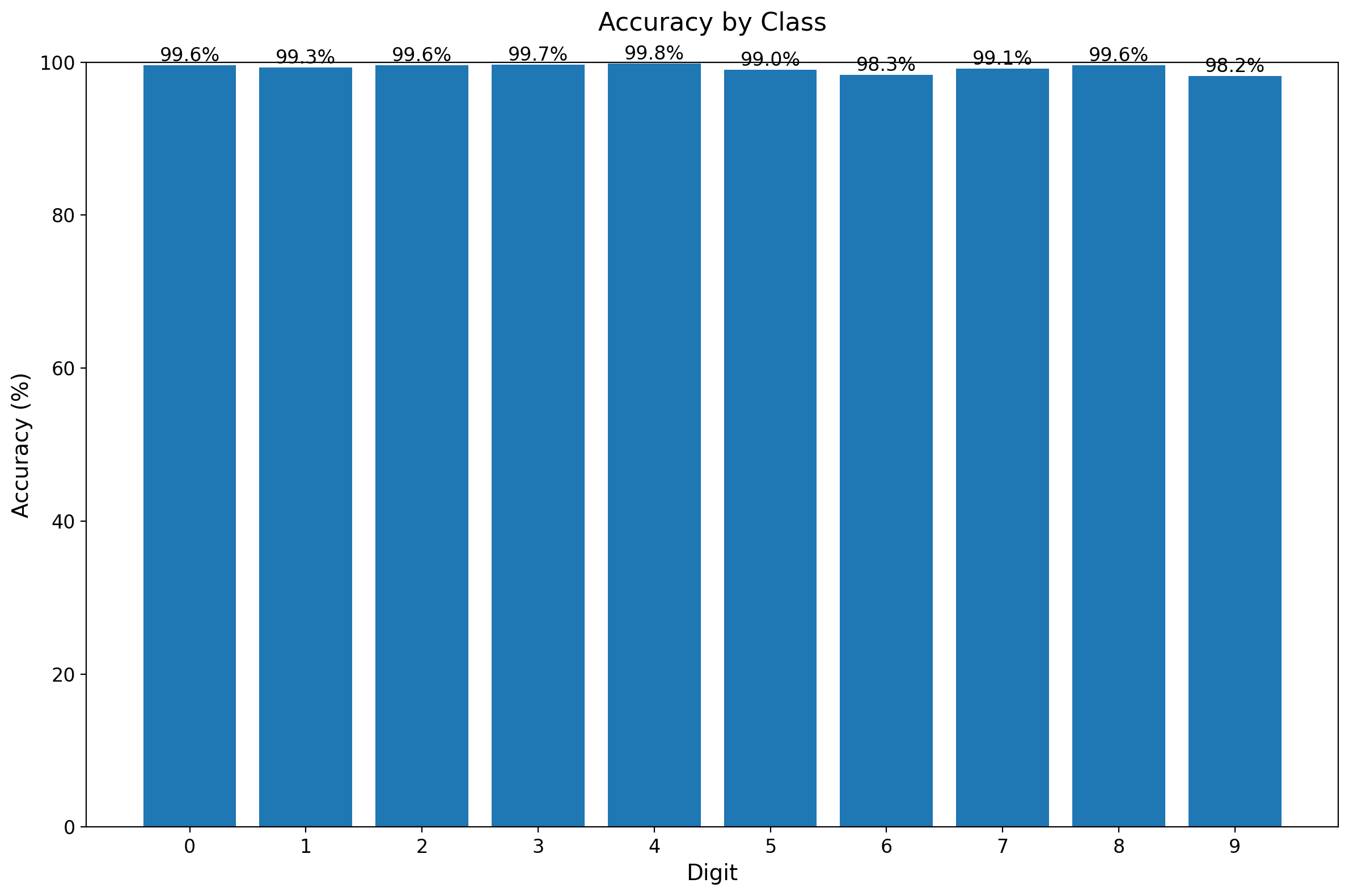
各数字识别准确率

从柱状图可以看出：

  • 大多数数字的识别准确率都在99%以上
  • 某些数字（如1和7）的识别准确率特别高
  • 某些数字（如9）的识别准确率相对较低，这可能是因为它们的书写变化较大

5. 深入理解与讨论

5.1 CNN特征学习机制

通过上面的实验结果，我们看到模型达到了很高的识别准确率。那么，CNN是如何实现这个看似简单的任务的呢？让我们通过这个项目深入理解深度学习的工作原理。

在我们的项目中，CNN通过三层卷积网络逐步学习图像特征：

  1. 第一卷积层（Conv1）提取基本特征：

    • 32个3×3卷积核提取边缘、角点等低级特征
    • 特征图显示了数字的基本轮廓
    • 这一层主要关注局部像素变化

  2. 第二卷积层（Conv2）组合特征：

    • 64个卷积核组合低级特征，形成更复杂的模式
    • 特征图开始显示数字的部分结构
    • 感受野扩大，可以检测更复杂的模式

  3. 第三卷积层（Conv3）提取高级特征：

    • 128个卷积核捕捉完整的数字结构
    • 特征图展示了数字的关键识别特征
    • 此时已经能够表示完整的数字形状

这种层次化的特征提取过程是深度学习区别于传统机器学习的关键所在。每一层都在前一层的基础上提取更抽象的特征，最终形成对数字的完整理解。

5.2 任务特点与挑战

MNIST手写数字识别虽然是一个相对简单的计算机视觉任务，但它仍然具有一些特点和挑战：

  1. 变化多样性：同一个数字可以有多种不同的书写风格
  2. 噪声和变形：手写数字可能存在噪声、倾斜或变形
  3. 特征提取：需要从28×28的像素矩阵中提取有意义的特征
  4. 类别区分：某些数字（如4和9，3和8）在某些书写风格下非常相似

我们的CNN模型通过层次化特征学习和非线性变换，成功应对了这些挑战，实现了高精度的识别。

6. 总结与未来方向

通过这个手写数字识别项目，我们不仅实现了一个高精度的分类器，更重要的是理解了深度学习在实际应用中的工作方式：

  1. 自动特征学习：CNN能够自动从原始像素数据中学习有用的特征表示，无需人工设计特征提取器
  2. 层次化表示：从低级边缘特征到高级结构特征，CNN通过多层结构逐步构建复杂的表示
  3. 端到端优化：通过反向传播算法，模型能够端到端地优化所有参数，使整个系统协同工作

这个项目虽然简单，但包含了深度学习的核心思想和方法。通过理解CNN如何解决MNIST这样的基础任务，我们可以更好地把握深度学习的本质，为解决更复杂的计算机视觉问题打下基础。

完整代码

完整的项目代码已经上传到GitHub：mnist-pytorch

项目包含：

  • 完整的模型实现
  • 训练和测试代码
  • 可视化工具
  • 详细的文档说明

如果这个项目对您有帮助，欢迎给仓库点个star⭐️。如有任何问题或建议，也欢迎在评论区留言交流。